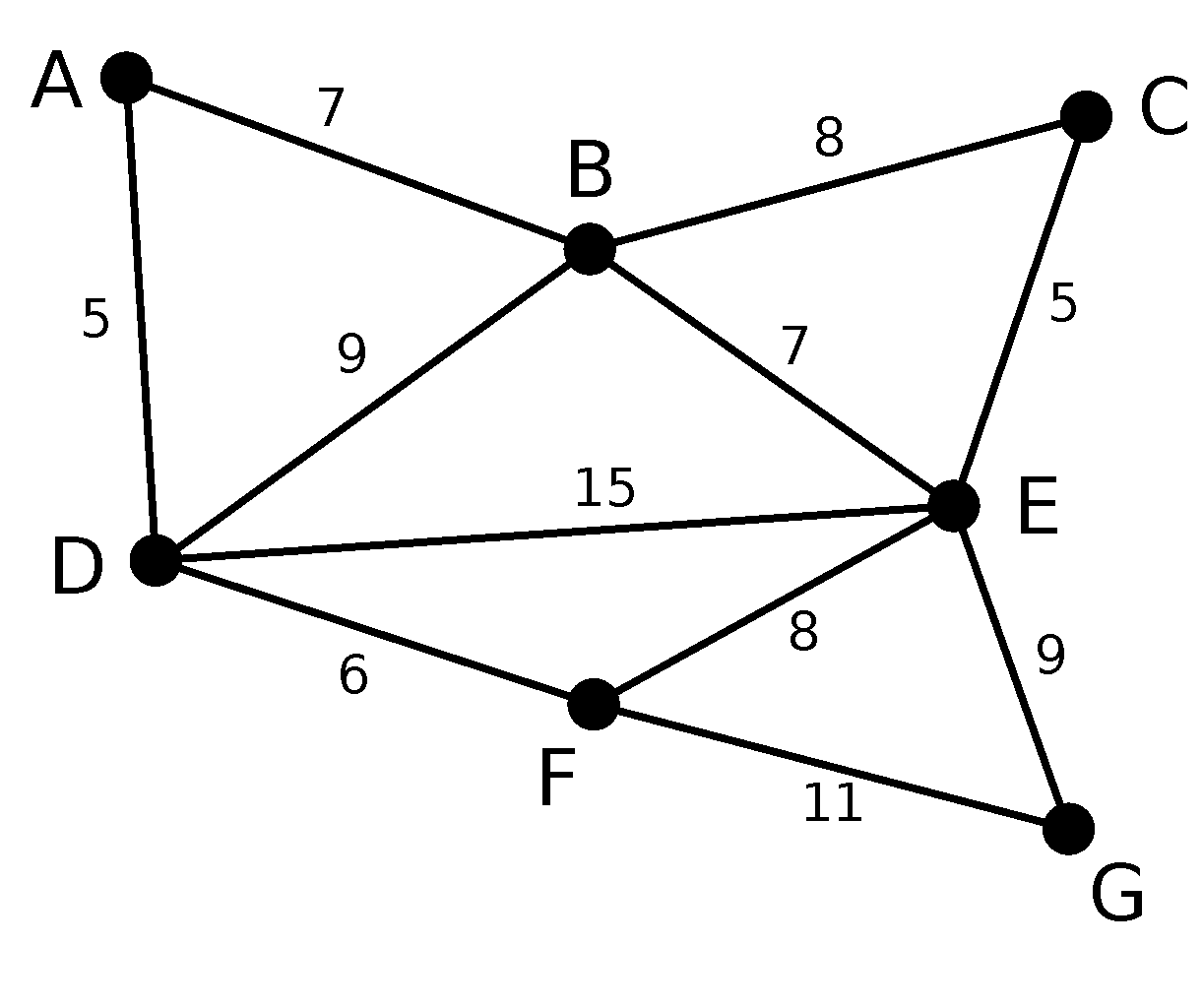
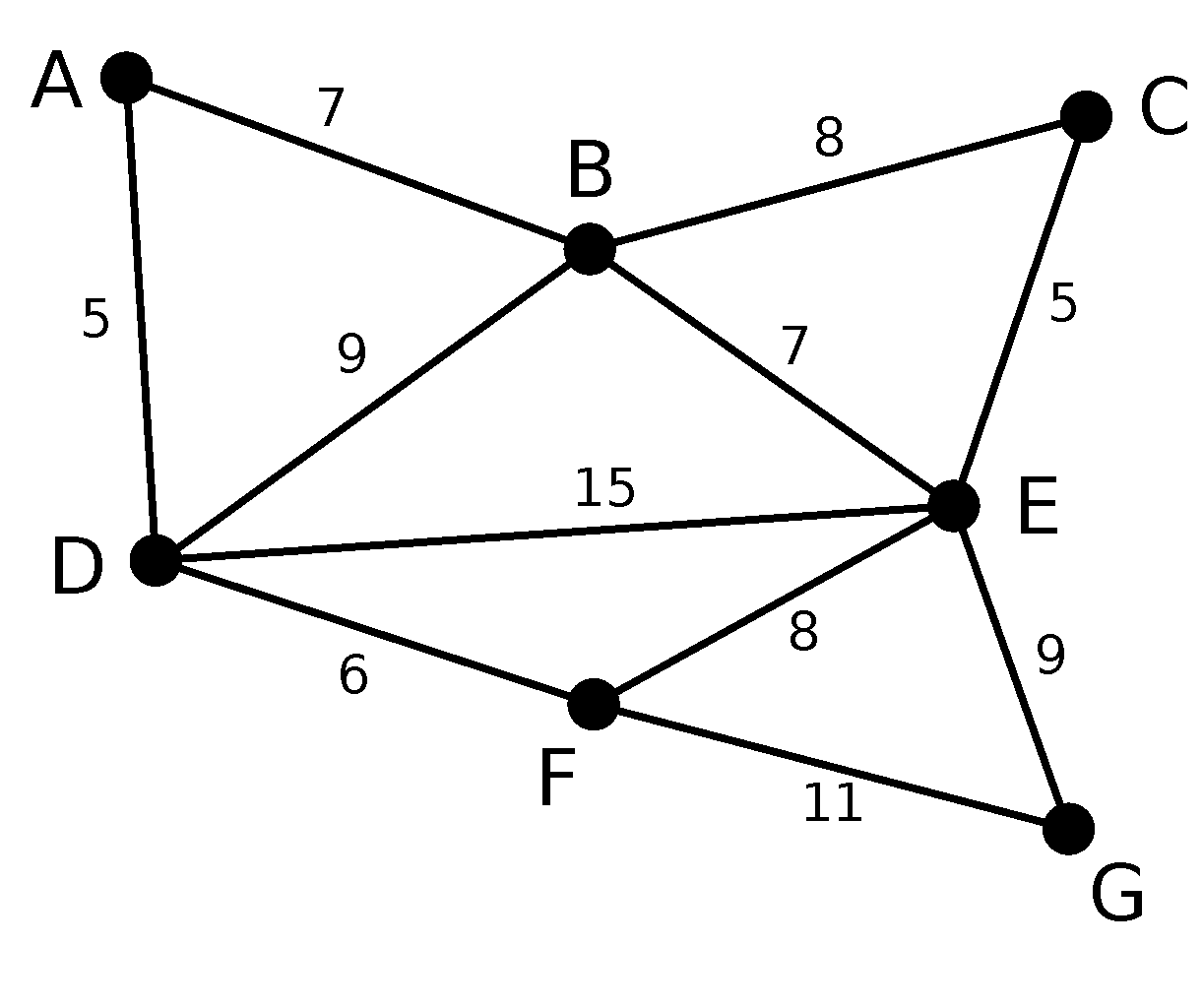
最小生成树

Kruscal 算法

Kruskal 算法的基本思想是从小到大加入边，即按边贪心。

实现

假设连通网 $N = ( V , E )$ ，将 $N$ 中的边按权值从小到大的顺序排列。

① 初始状态为只有 $n$ 个顶点而无边的非连通图 $T = ( V , { } )$ ，图中每个顶点自成一个连通分量。

② 在 $E$ 中选择权值最小的边，若该边依附的顶点落在 $T$ 中不同的连通分量上（即不形成回路），则将此边将入到 $T$ 中，否则舍去此边而选择下一条权值最小的边。

③ 重复 ②，直到 $T$ 中所有的顶点都在同一连通分量上为止。

算法虽简单，但需要相应的数据结构来支持。 具体来说，我们需要维护一个森林，其中包含以下两个操作

• 查询两个结点是否在同一棵树中
• 连接两棵树

本质上这就是查询两点是否连通和连接两点的操作， 因而我们可以使用并查集维护。

以下为 C++ 实现

• 用结构体储存边便于排序
• 用并查集维护连通关系

#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;

struct edge {
  int u, v, w;
  edge(int u, int v, int w) : u(u), v(v), w(w) {}
  friend bool operator<(edge a, edge b) { return a.w < b.w; }
};

int n, m;
vector<edge> edges;
vector<int> parent;

int find(int x) {
  int cur = x, nxt;
  while (x != parent[x]) {
    x = parent[x];
  }
  while (cur != x) {
    nxt = parent[cur];
    parent[cur] = x;
    cur = nxt;
  }
  return x;
}

void merge(int x, int y) {
  x = find(x), y = find(y);
  if (x != y) {
    parent[x] = y;
  }
}

int Kruscal() {
  int ans = 0, cnt = 0;
  // 将边按权值升序排序
  sort(edges.begin(), edges.end());

  int eu, ev;
  for (auto &e : edges) {
    eu = find(e.u);
    ev = find(e.v);
    // 如果两个点不连通， 则需要加边
    if (eu != ev) {
      ans += e.w;
      merge(ev, eu);
      // 连通(合并) eu, ev
      parent[ev] = eu;
      ++cnt;
      if (cnt == n - 1) {
        break;
      }
    }
  }
  if (cnt != n - 1) {
    ans = -1;  // 无法生成最小生成树
  }
  return ans;
}

int main() {
  cin >> n >> m;
  for (int i = 0; i < m; ++i) {
    int u, v, w;
    cin >> u >> v >> w;
    edges.emplace_back(u, v, w);
  }
  for (int i = 0; i <= n; ++i) {
    parent.push_back(i);
  }

  cout << Kruscal() << endl;
  return 0;
}

Prim 算法

Prim 算法是另一种常见并且好写的最小生成树算法。该算法的基本思想是从一个结点开始，不断加点（而不是 Kruskal 算法的加边）。

实现

具体来说，每次要选择距离最小的一个结点，以及用新的边更新其他结点的距离。

其实跟 Dijkstra 算法一样，每次找到距离最小的一个点，可以暴力找也可以用堆维护。

堆优化的方式类似 Dijkstra 的堆优化，但如果使用二叉堆等不支持 $O(1)$ decrease-key 的堆，复杂度就不优于 Kruskal，常数也比 Kruskal 大。所以，一般情况下都使用 Kruskal 算法，在稠密图尤其是完全图上，暴力 Prim 的复杂度比 Kruskal 优，但 不一定 实际跑得更快。

• 暴力: $O(n^2 + m)$
• 二叉堆: $O((n + m)\log n)$
• Fib 堆: $O(n\log n + m)$