AVL树(平衡二叉树)

前言

平衡二叉树和 AVL 树这两个概念的区分：平衡二叉树是对这样一种数据结构的定义，是一种描述；而 AVL 树则是对这样子一种数据结构的实现。同红黑树和 B 树等一样，都是对这样一种结构的实现，同时都是具有自平衡特性的。

AVL 树是最早的被发明的自平衡二叉树, 得名于其发明者Adelson-Velskii(AV) 和 Landis(L)。

定义

AVL 树是带有平衡条件的二叉查找树，一般是用平衡因子差值判断是否平衡并通过旋转来实现平衡，左右子树树高不超过 1。

平衡因子: 左子树的高度 - 右子树的高度 (因而可正可负)

提示

基于平衡因子，我们就可以这样定义 AVL 树为所有结点的平衡因子的绝对值都不超过 1 的二叉树。

和红黑树相比，AVL 树是严格的平衡二叉树，平衡条件必须满足所有节点的左右子树高度差的绝对值不超过 1。不管我们是执行插入还是删除操作，只要不满足上面的条件，就要通过旋转来保持平衡，而旋转是非常耗时的，由此我们可以知道 AVL 树适合用于插入与删除次数比较少，但查找多的情况

性质

1. 空二叉树是一个 AVL 树
2. 如果 T 是一棵 AVL 树，那么其左右子树也是 AVL 树，并且 $| h(\text{ls})-h(\text{rs}) | \leqslant 1$, $h$ 是其左右子树的高度
3. 树高为$O(\log n)$

备注

树高的证明

设 $f_n$ 为高度为 $n$ 的 AVL 树所包含的最少节点数，则有

$$f_{n}= \begin{cases}1 & (n=1) \\ 2 & (n=2) \\ f_{n-1}+f_{n-2}+1 & (n>2)\end{cases}$$

显然$\{ f_n + 1 \}$是一个斐波那契数列。众所周知，斐波那契数列是以指数的速度增长的，因此 AVL 树的高度为$O(\log n)$ 。

操作

插入结点

与 BST（二叉搜索树）中类似，先进行一次失败的查找来确定插入的位置，插入节点后根据平衡因子来决定是否需要调整。

删除结点

删除和 BST 类似，将结点与后继交换后再删除。

删除会导致树高以及平衡因子变化，这时需要沿着被删除结点到根的路径来调整这种变化。

旋转

平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的。根据旋转的方向有两种处理方式，左旋与右旋 。

最小失衡子树：在新插入的结点向上查找，以第一个平衡因子的绝对值超过 1 的结点为根的子树称为最小不平衡子树。也就是说，一棵失衡的树，是有可能有多棵子树同时失衡的。而这个时候，我们只要调整最小的不平衡子树，就能够将不平衡的树调整为平衡的树。

提示

旋转不改变树的序

左旋

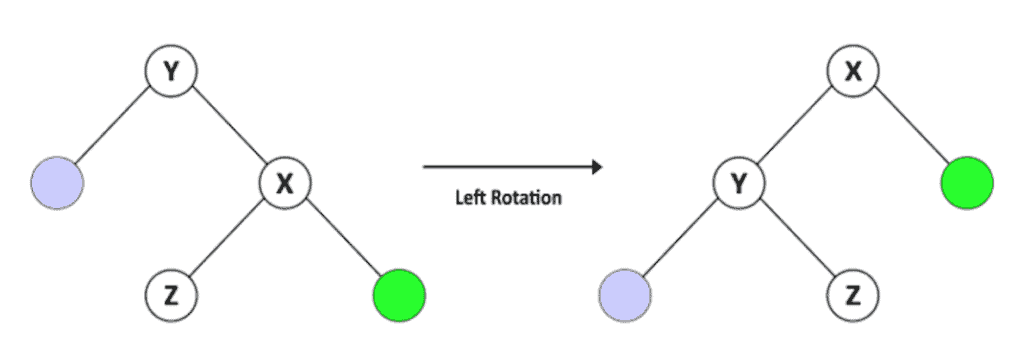
假设我们有一棵元素为字母二叉搜索树 $T_1$ , 其根节点为 Y, X 是 Y 的右儿子，Z 是 X 的左儿子, 当前的树给出的顺序为 Y < Z < X,

对 Y 左旋后, 可得树 $T_2$ 如下图所示，观察可知 $T_2$ 仍是一个保留了 Y < Z < X 顺序的二叉搜索树

右旋

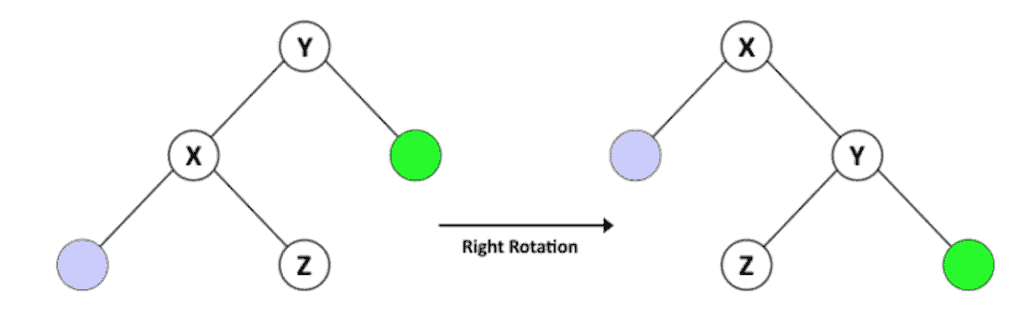
假设我们有一棵元素为字母二叉搜索树 $T_1$ , 其根节点为 Y, X 是 Y 的左儿子，Z 是 X 的右儿子, 当前的树给出的顺序为 X < Z < Y,

对 Y 右旋后, 可得树 $T_2$ 如下图所示，观察可知 $T_2$ 仍是一个保留了 X < Z < Y 顺序的二叉搜索树

平衡的维护

我们先定位到最小失衡子树，分以下4种情况进行旋转

第一类: 右子树更高

1. 右子树的右儿子高

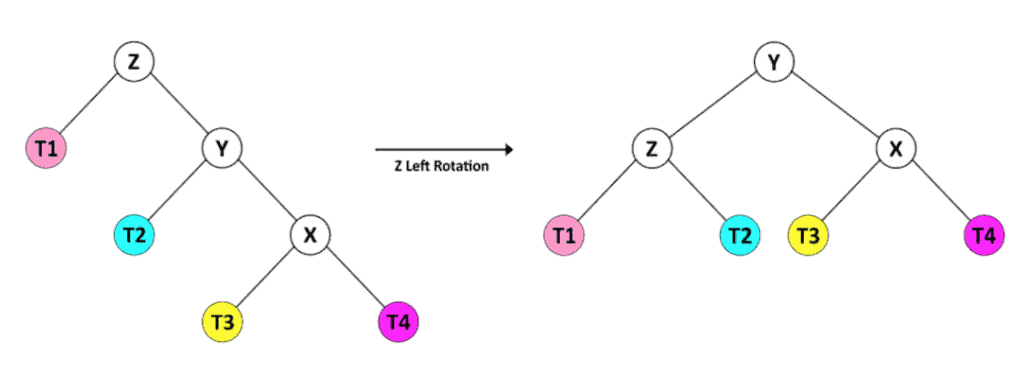
2. 右子树的左儿子高

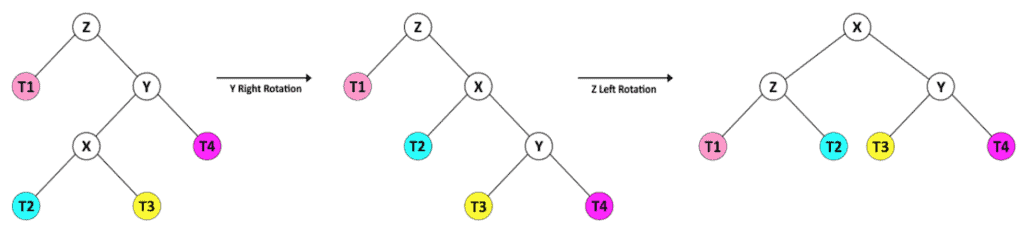
第二类: 左子树更高

3. 左子树的左儿子高

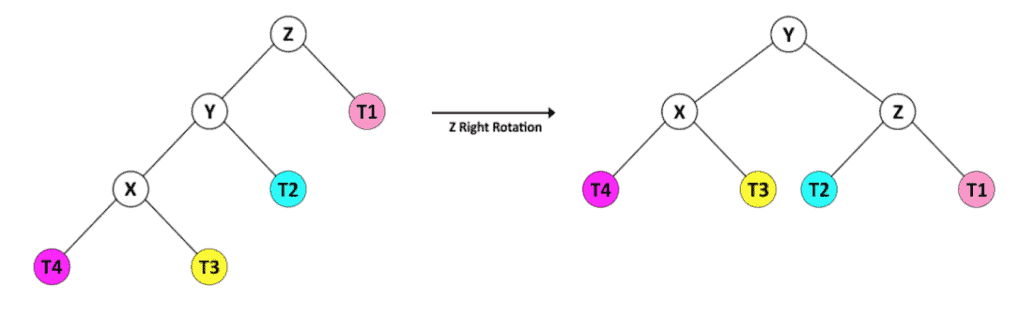
4. 左子树的右儿子高

通过对 Y 结点 进行一次左旋，使其变为和 3 一样型构

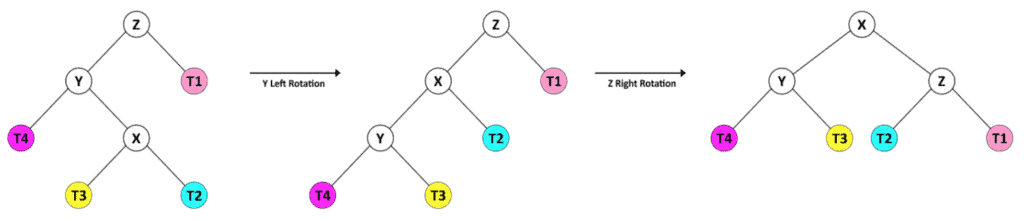
可视化

在 AVL Tree Visualization 可以观察 AVL 树维护平衡的过程。