O(nlog(n)) 算法

1. 希尔排序 (不稳定)

希尔排序是由美国辛辛那提大学的数学系博士 Donald Shell 提出的排序算法， 也是首批将时间复杂度降到 $O(n^2)$ 以下的算法之一。 虽然原始的希尔排序最坏时间复杂度仍然是 $O(n^2)$ ，但经过优化的希尔排序可以达到 $O(n^{1.3})$ 甚至 $O(n^{7/6})$。

希尔排序本质上是对插入排序的一种优化，它利用了插入排序的简单，又克服了插入排序每次只交换相邻两个元素的缺点。它的基本思想是：

• 将待排序数组按照一定的间隔分为多个子数组，每组分别进行插入排序。这里按照间隔分组指的不是取连续的一段数组，而是每跳跃一定间隔取一个值组成一组
• 逐渐缩小间隔进行下一轮排序
• 最后一轮时，取间隔为 1，也就相当于直接使用插入排序。但这时经过前面的「宏观调控」，数组已经基本有序了，所以此时的插入排序只需进行少量交换便可完成

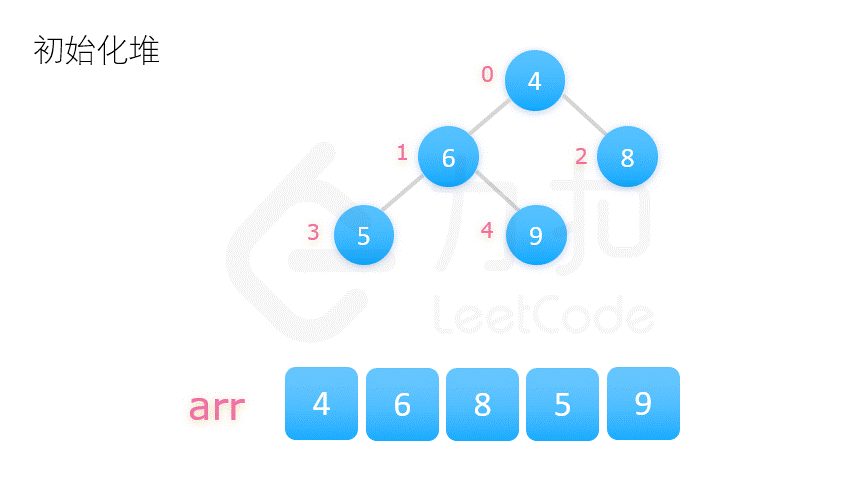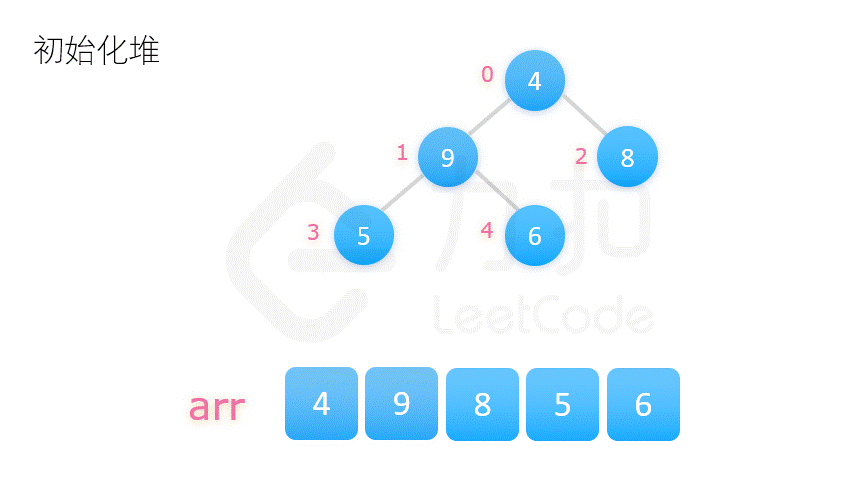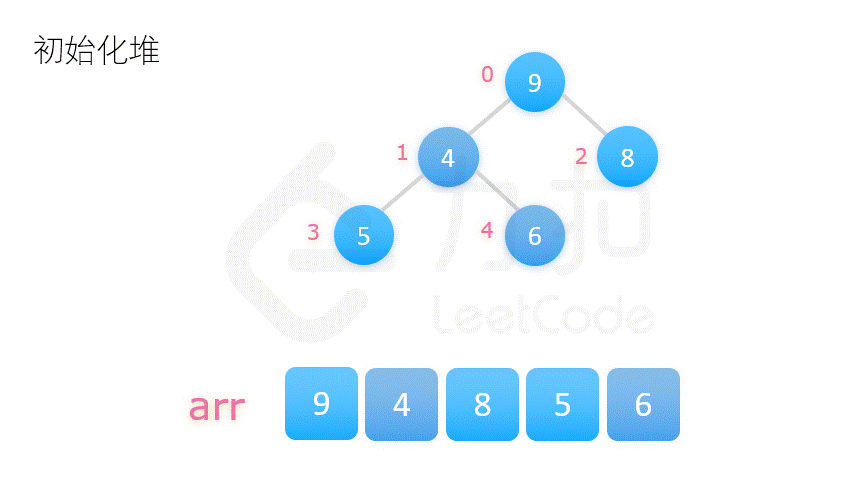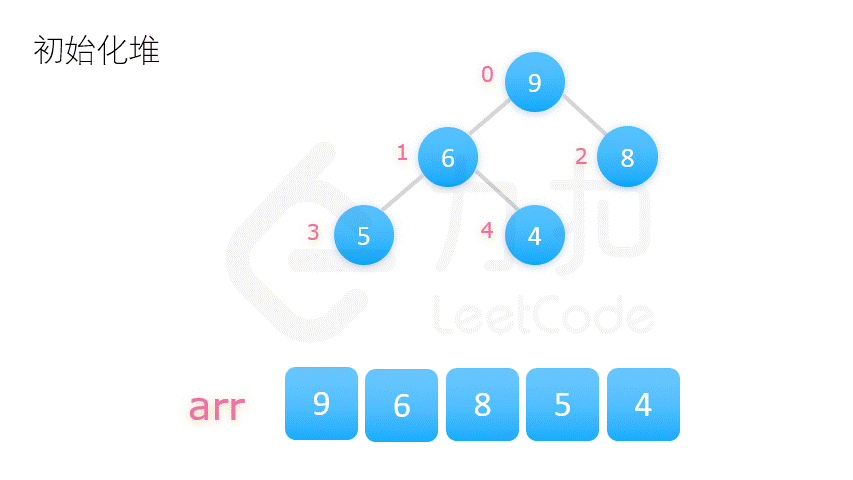
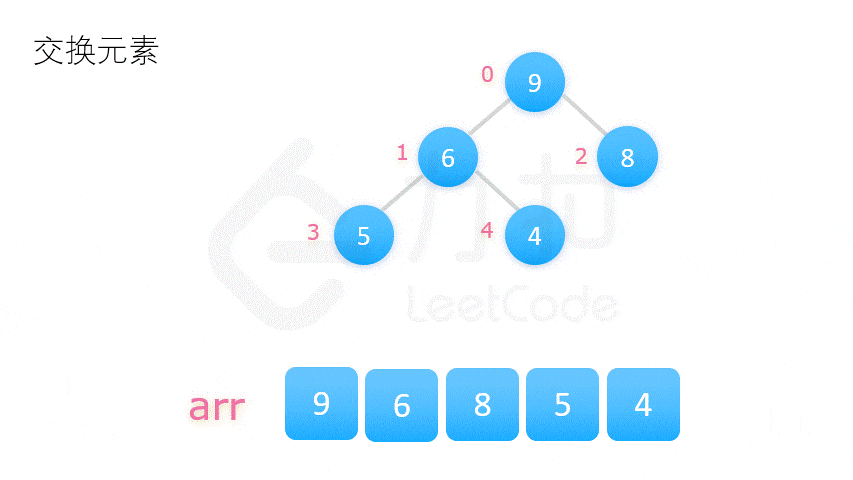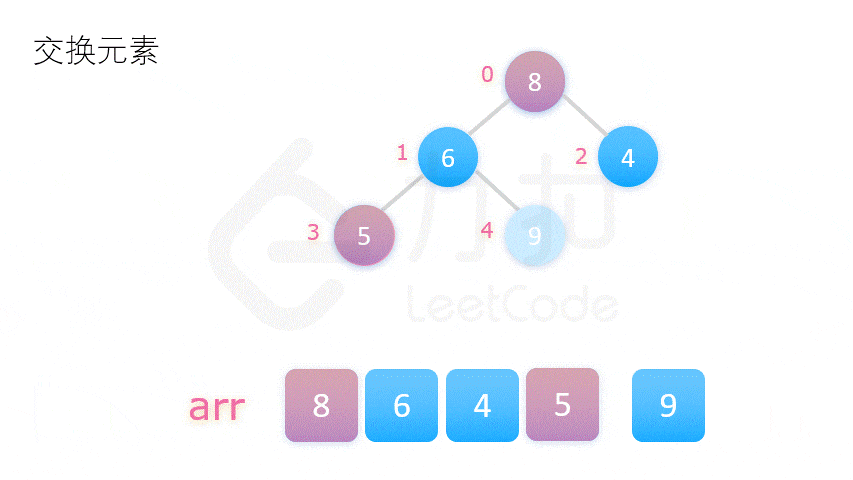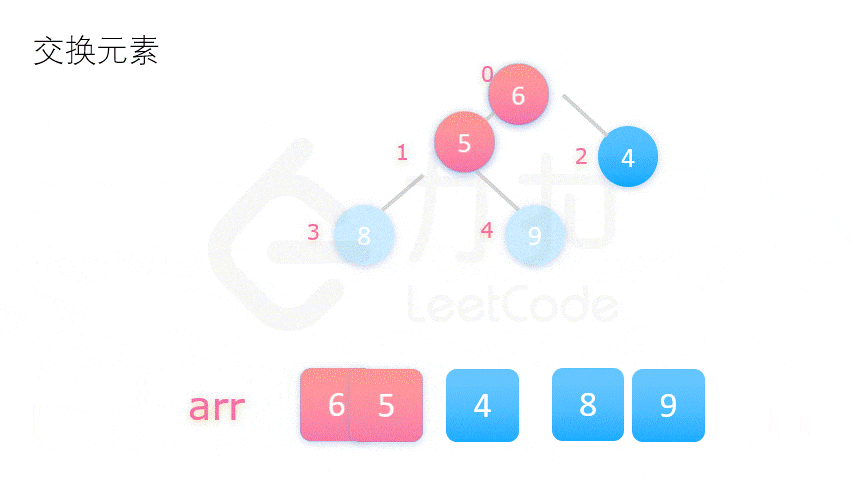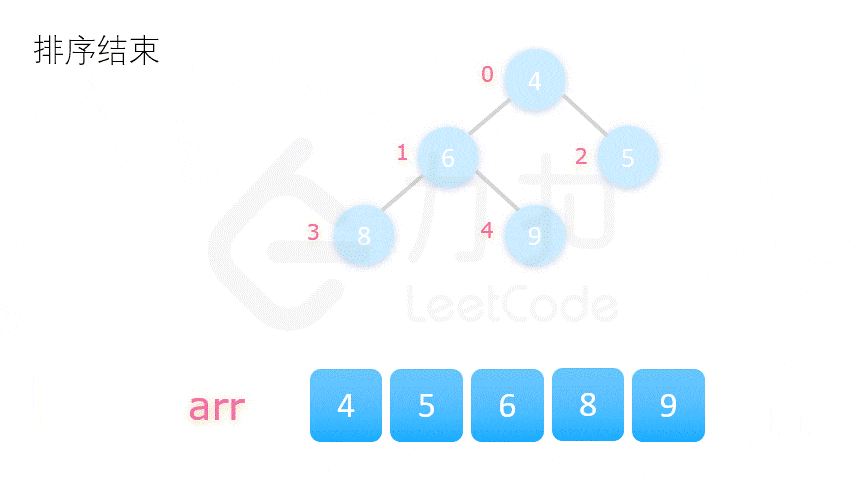
2. 堆排序 (不稳定)

void maxHeapify(vector<int>& arr, int i, int heapSize) {
  int l = 2 * i + 1, r = 2 * i + 2, largest = i;
  if (l < heapSize && arr[l] > arr[largest]) {
    largest = l;
  }
  if (r < heapSize && arr[r] > arr[largest]) {
    largest = r;
  }
  if (largest != i) {
    swap(arr[i], arr[largest]);
    maxHeapify(arr, largest, heapSize);
  }
}

void buildMaxHeap(vector<int>& arr) {
  int n = arr.size();
  for (int i = n / 2; i >= 0; --i) {
    maxHeapify(arr, i, n);
  }
}

void heapSort(vector<int>& arr) {
  buildMaxHeap(arr);
  for (int heapsize = arr.size() - 1; heapsize > 0; --heapsize) {
    swap(arr[0], arr[heapsize]);
    maxHeapify(arr, 0, heapsize);
  }
}

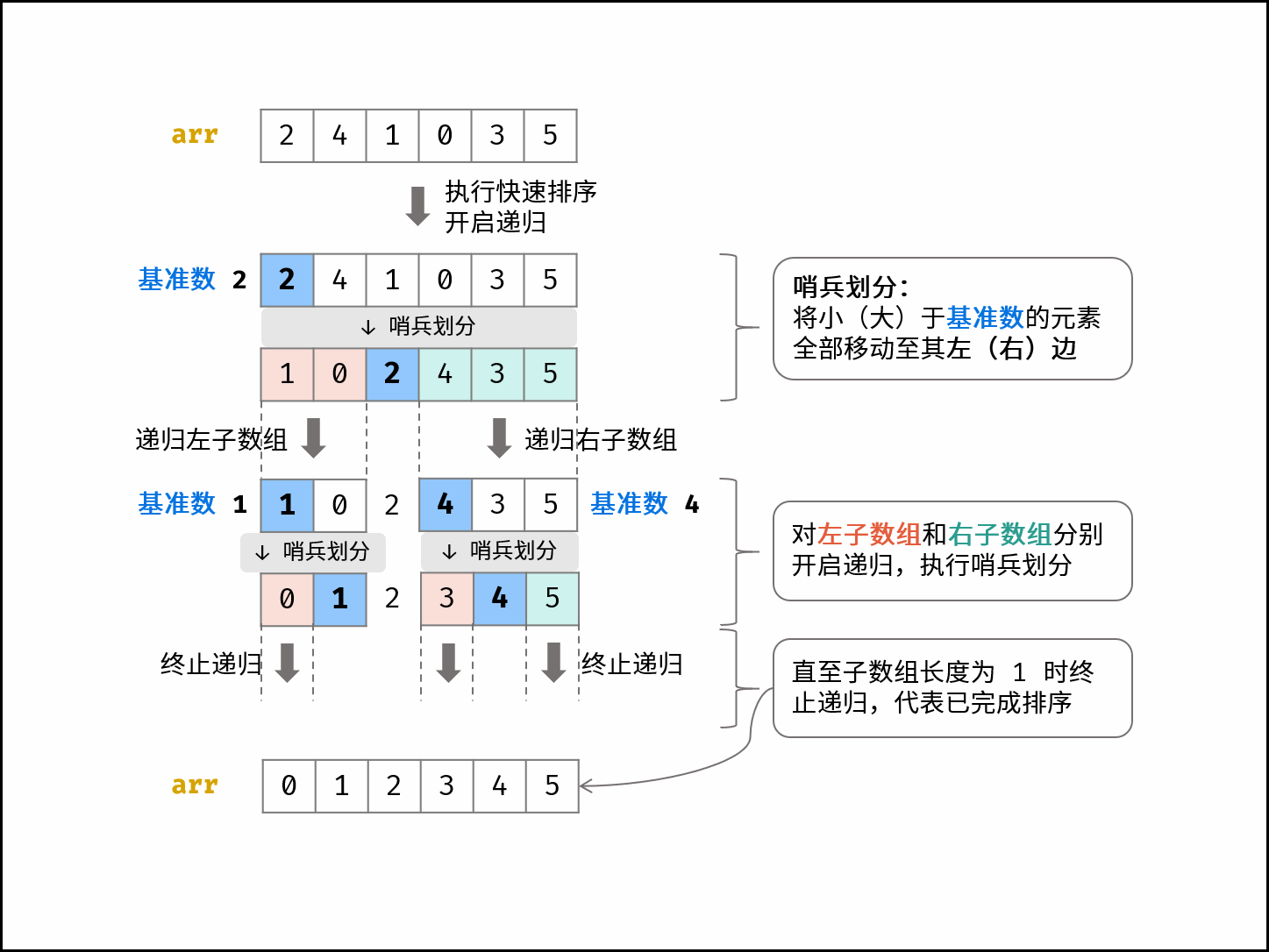
3. 快速排序 (不稳定)

如下图所示，为数组 [2,4,1,0,3,5] 的快速排序过程。

朴素实现

int partition(vector<int>& nums, int l, int r) {
  // 以 nums[l] 作为基准数
  int i = l, j = r;
  while (i < j) {
    while (i < j && nums[j] >= nums[l]) j--;
    while (i < j && nums[i] <= nums[l]) i++;
    swap(nums[i], nums[j]);
  }
  swap(nums[i], nums[l]);
  return i;
}

void quickSort(vector<int>& nums, int l, int r) {
  // 子数组长度为 1 时终止递归
  if (l >= r) return;
  // 哨兵划分操作
  int i = partition(nums, l, r);
  // 递归左（右）子数组执行哨兵划分
  quickSort(nums, l, i - 1);
  quickSort(nums, i + 1, r);
}

合并partition函数和quickSort函数，并加入 base 随机化可得

/* srand(time(NULL)) is needed */
void qsort(vector<int>& nums, int left, int right) {
  if (left > right) {
    return;
  }
  int i = left;
  int j = right;
  // nums[left] is base
  //引入随机base避免退化成冒泡
  swap(nums[left], nums[rand() % (right - left + 1) + left]);

  while (i < j) {
    /* --j 和 ++i 的顺序不能调换 ! */
    while (i < j && nums[j] >= nums[left]) --j;
    while (i < j && nums[i] <= nums[left]) ++i;
    swap(nums[i], nums[j]);
  }
  swap(nums[left], nums[i]);

  qsort(nums, left, i - 1);
  qsort(nums, i + 1, right);
}

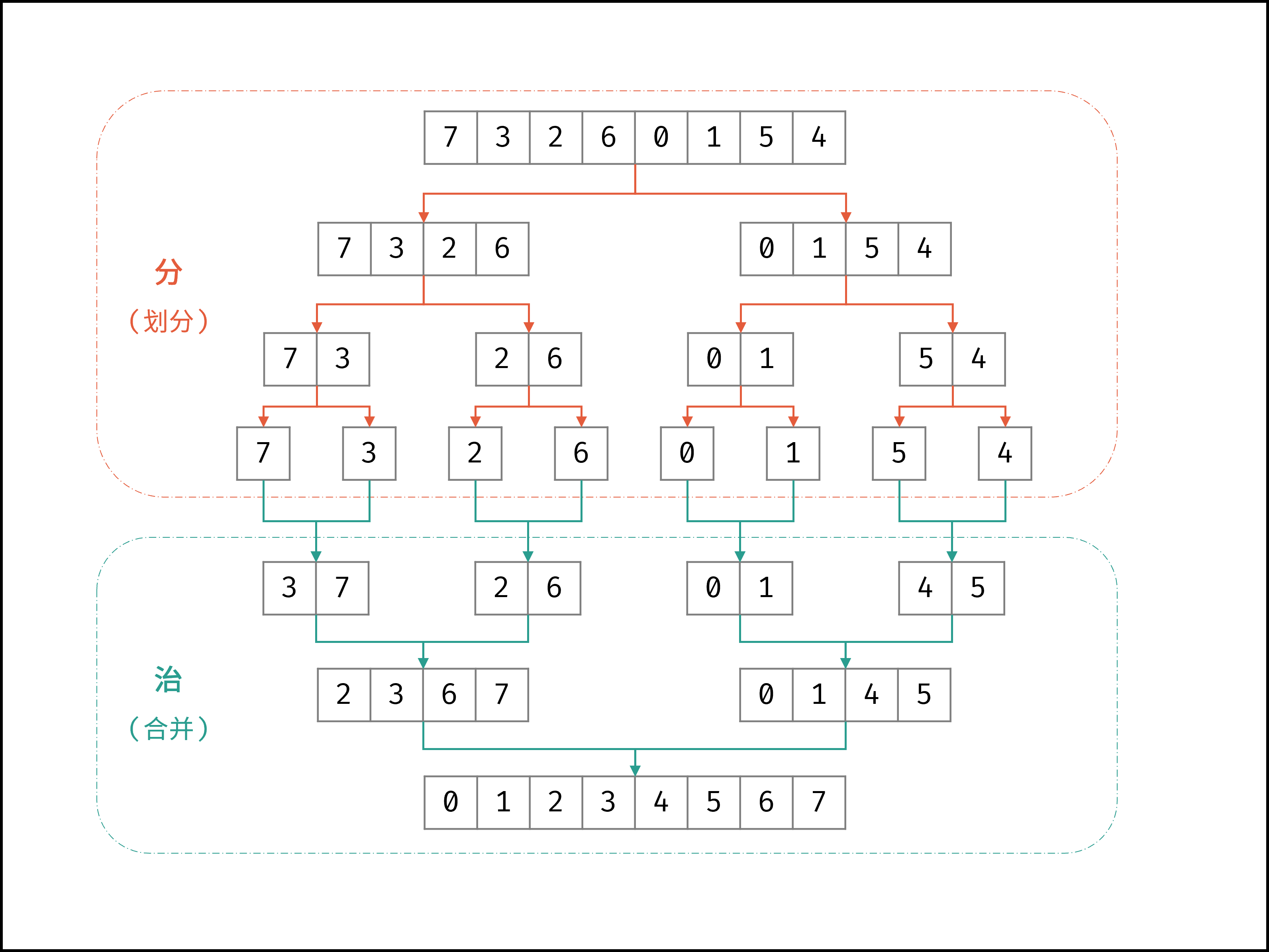
4. 归并排序 (稳定)

如下图所示，为数组 [7,3,2,6,0,1,5,4] 的归并排序过程。

void mergeSort(vector<int>& nums, int l, int r) {
  // 终止条件
  if (l >= r) {
    return;
  }
  // 递归划分, 定义暂存区
  int m = (l + r) / 2, cache[r - l + 1];
  // 对左右区间分别排序
  mergeSort(nums, l, m);
  mergeSort(nums, m + 1, r);
  // 合并阶段，暂存需合并元素
  for (int k = l; k <= r; k++) {
    cache[k - l] = nums[k];
  }
  int i = 0, j = m - l + 1;  // 两指针分别指向左/右子数组的首个元素
  for (int k = l; k <= r; k++) {  // 遍历合并左/右子数组
    if (i >= m - l + 1) {
      nums[k] = cache[j++];
    } else if (j >= r - l + 1 || cache[i] <= cache[j]) {
      nums[k] = cache[i++];
    } else {
      nums[k] = cache[j++];
    }
  }
}