NP 完全性
推荐阅读文章https://www.baeldung.com/cs/p-np-np-complete-np-hard
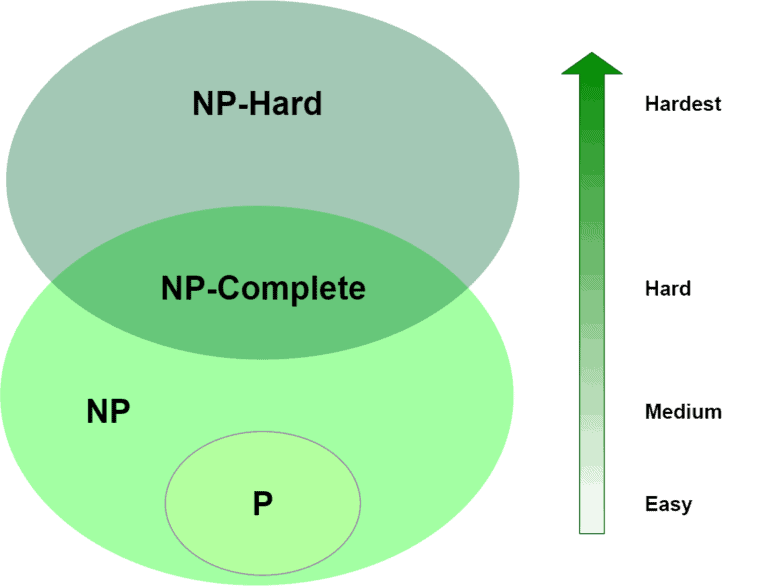
概念
P 类问题
P 类问题就是多项式时间内可以解决的问题。 更为确切的说, 这些问题可以在时间 内解决, 其中 为某一常量, 是此问题输入的规模。 常见的问题很多都是 P 类问题, 比如
- 素数测试 (Testing for primacy)
- 哈希表的查找, 字符串操作, 排序问题
- 线性搜索和二分搜索
- 最短路问题 (Bellman-Ford, Dijkstra, Floyd-Warshall)
NP 类问题
NP 问题是多项式时间内不可解的, 但是可以在多项式时间内被验证。即给定一个解, 我们可以在多项式时间内验证它的正确性。如:
- 质因数分解 (Integer Factorization)
- 图同构 (Graph Isomorphism)
NPC 类问题
一个NPC问题需要同时满足两个条件:① 该问题是NP问题;② NP里所有问题可以在多项式时间内归约到该问题。
- 旅行商判定问题 (Traveling Salesman)
- 0/1背包判定问题 (Knapsack)
- 图染色判定问题 (Graph Coloring)
NP 难问题
满足 NPC问题的条件 ② : NP里所有问题可以在多项式时间内归约到该问题
- 旅行商问题 (Traveling Salesman)
- 背包问题 (Knapsack)
- 图染�色 (Graph Coloring)
多项式时间
抽象问题
定义抽象问题 Q 为在问题实例集合 I 和问题解集合 S 上的一个二元关系。
例如, 最短路问题的一个实例是由一个图和两个顶点所组成的三元组, 其解为图中的顶点序列, 序列可能为空(两个顶点间不存在通路)。 最短路问题本身就是一个关系, 它把图的每个实例和两个顶点与图中联系这两个顶点的最短路径联系在了一起, 因为最短路径不一定是唯一的, 因此, 一个给定的问题实例可能有多个解。
为了简单起见, NP 完全性问题主要考察的是判定问题, 即那些解为是或否的问题。 于是, 我们可以把抽象的判定问题看做是从实例集 I 映射到解集 上的一个函数
例如路径存在问题, 如果 是判定问题 PATH 的一个实例, 那么若从 到 的最短路径的长度至多为 条边, 则 PATH(i)=1 (是), 否则 PATH(i)=0 (否)
许多抽象问题并不是判定问题, 而是最优化问题, 在这些问题中, 某些量必须被最大化或者最小化。